
从单词来看,
Array 很好理解一批一批的意思;
Set 含义比较多,常见有放、集合、一套...;

从字面来记忆它们的区别,Array就是一批一批的,Set是特意放入、采集进去的,所以Array不区分重复,Set区分重复。
下面是是将《秒懂算法:用常识解读数据结构》第一章的内容拷贝来这里,做了一些编辑。
数组示例:
array = ["apples", "bananas", "cucumbers", "dates", "elderberries"]
术语:

数组的操作:
CURD
速度计量:
衡量操作的速度也被称作衡量其时间复杂度。
不同人会混用速度、时间复杂度、效率、性能以及运行时间这几个术语。一般来说,它们指的都是一个操作所需要的步骤数。
O(1):常数复杂度,表示无论输入规模如何增长,算法的执行时间都保持不变。
PS:不管有多少数据,读取都是一个步骤。
为什么?
我们在在创建和使用数组的时候,只会关注数组的大小和索引,
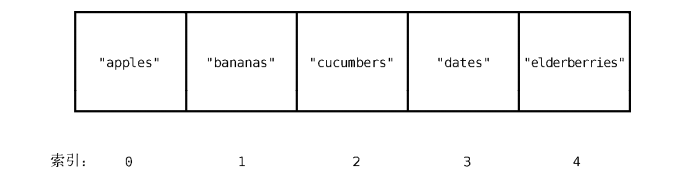
但是数组在计算机的底层,它在操作的时候,还需要一个内存地址,下面展示数据、内存地址和索引的关系,

以上的图示,基本就能解释了为什么计算机只用 1 步就能找到数组的第一个值。计算机只要再做一个简单的加法,就能找到任意索引的值。
如果让计算机寻找索引 3 的值,那么它只需在索引 0 的内存地址上加 3 即可。(毕竟内存地址是连续的。)
O(n):线性复杂度。表示算法的执行时间与输入规模成线性关系。
还是以之前的数组为例。计算机无法立刻弄清每个格子的内容。对计算机来说,
这个数组看起来就像下面示例这样。
【?,?,?,?,?】
比如说需要它去找
dates
这个数据,那么就步骤如下,
会第0索引开始找dates这个数据,
需要明白的是在Array里,插入到数组的最后一列,和从中间插入是两种不同的操作。
最后一列插入

一旦计算机算出了存储新值的内存地址,它只需要 1 步就能完成插入。
下图展示了在数组末尾插入"figs"的过程。

so, O(1):常数复杂度,表示无论输入规模如何增长,算法的执行时间都保持不变。
中间插入
假设我们要在索引 2 处插入"figs"。先来看下图,
为此,需要向右移动"cucumbers"、"dates"和 "elderberries"来给"figs"腾出空间。这
个过程需要多步,因为需要先把"elderberries"向右移动一个格子,才能移动"dates"。然后,
再移动"dates"来给"cucumbers"让位。
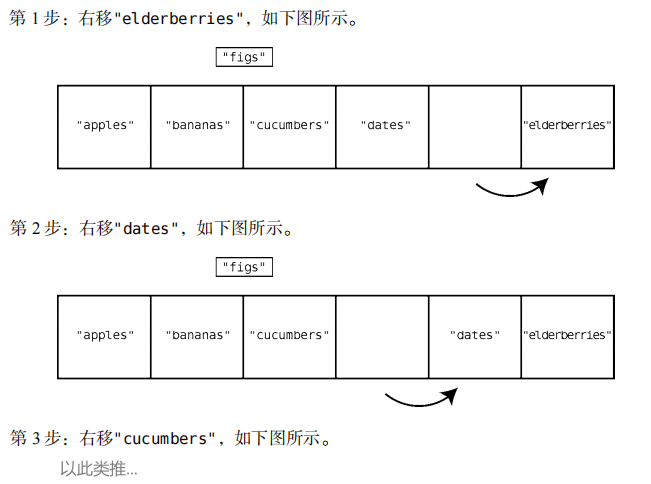
在这个例子中,插入需要 4 步,其中 3 步是数据右移,剩下 1 步是插入新值。
向数组开头插入元素需要步数最多,也就是所谓的最坏情况。
这是因为要在数组开头插入元
素,必须把其他所有值都右移一个格子。
对包含 N 个元素的数组来说,最坏的情况下需要 N + 1 步插入。这是因为需要移动 N 个元
素,然后才能执行插入操作。
so, O(n+1):线性复杂度。表示算法的执行时间与输入规模成线性关系。
删除指的是删去特定索引的值的过程。
下面以删除购物清单数组索引 2 处的值为例。在这个数组中,这个值是"cucumbers"。

严格意义上来说,删除"cucumbers"只需 1 步。但有一个问题:数组中间有了一个空格子。
中间有空格子的数组是无效的。
要解决这个问题,需要把"dates"和"elderberries"左移。因此删除操作还需要额外步骤。

这个删除操作用了 3 步。1 步是删除元素,另外 2 步是移动元素来填补空格子。
和插入一样,删除元素的最坏情况是删除数组中的第一个元素。因为索引 0 会变成空格子,
所以必须把剩余的所有元素都左移。
so, O(n+1):线性复杂度。表示算法的执行时间与输入规模成线性关系。
why is Set ?
集合的定义是,集合中包含的元素不能重复。
集合有多种类型,但本节只讨论基于数组的集合。这种集合和数组很相似,它们都是存储值
的简单列表,二者的唯一区别在于,不能往集合中插入重复的值。
假设已知集合["a", "b", "c"],而你想再添加一个"b"。因为"b"已经存在于集合中,所以计算机会拒绝这次操作。
当需要确保数据不重复时,集合非常有用。
Set的操作:
CURD
集合的读取和数组的读取完全一致,即计算机检查特定索引处的值只需要 1 步。这是因为计
算机能跳转到集合内的任意索引,而这只需简单地计算并跳转到其内存地址即可。
集合的查找也和数组的查找没什么区别,即查找集合中的值最多需要 N 步。集合和数组的
删除操作也一模一样,即要删除一个值并移动其他数据来填空最多需要 N 步。
集合的插入和数组的插入则不同。先来看看在集合末尾插入值。这对数组来说只需要 1 步,
是最好的情况。
但集合不同,计算机需要先判断这个值是否存在于集合中——因为集合的规则是不允许插入
重复数据。
计算机要如何确保新数据不在集合中呢?
计算机一开始并不知道数组或者集合的格子中都存储了什么值。
因此,它必须先在集合中查找,才能知道要插入的值是否已经存在。只有集合中不存在这个新值的时候,计算机才能继续执行插入操作。(所以,所有的插入操作都需要先进行查找。)
来看一个例子。假设之前提到的购物清单是用集合存储的。这个假设很合理,因为我们不想
重复购物。假设集合目前是["apples", "bananas", "cucumbers", "dates", "elderberries"],
而我们想插入"figs"。
计算机必须执行以查找"figs"为首的如下操作:

"figs"不在索引 0 处,但可能在集合中的其他位置。在插入之前,需要确保"figs"也不在
这些位置。
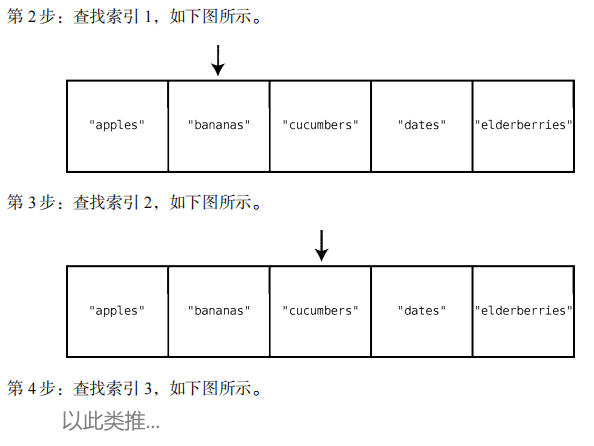
查找过整个集合后,我们确定其中没有"figs"。这时,就可以完成插入操作了。所以最后
一步如下。
第 6 步:在集合末尾插入"figs"。
最后插入
在集合末尾插入值是最好的情况,但对含有 5 个元素的集合来说仍然需要 6 步。换言之,必
须查找其全部 5 个元素之后才能执行插入操作。
换种说法:对包含 N 个元素的集合来说,在集合末尾插入值最多需要 N + 1 步。这是因为确
定集合中不含该值需要 N 步,而实际的插入还需要 1 步。数组的相同操作则只需要 1 步。
so, O(n+1):线性复杂度。表示算法的执行时间与输入规模成线性关系。
中间插入
向集合开头插入值是最坏的情况。为此,计算机需要先查找 N 个格子来确保该值不在集合
中,然后再用 N 步来右移全部数据,最后再用 1 步来插入新值。全部加起来是 2N + 1 步。
数组的相同操作则只需要 N + 1 步。
so, O(2n+1):线性复杂度。表示算法的执行时间与输入规模成线性关系。
集合和数组的删除操作也一模一样,即要删除一个值并移动其他数据来填空最多需要 N 步。
在Java中,想使用array和set,需要了解Collection,
Collection
|------List
| |------ArrayList
| |------LinkedList
| |------Vector
| |------Stack
|
|------Set
|------HashSet
| |------LinkedHashSet
|
|------SortedSet
|------TreeSet
|------NavigableSet
|------Queue
|------Deque
| |------ArrayDeque
| |------LinkedList
|------Map
|------HashMap
| |------LinkedHashMap
|
|------SortedMap
|------TreeMap
|------NavigableMap
如果从粗略的来看,
array 就是 ArrayList,
set 就是 TreeSet。